Have you ever wondered how things grow? From a simple seed sprouting into a mighty oak to the rapid spread of a virus across the globe, the concept of growth is woven into the fabric of our world. Two mathematical models, quadratic and exponential, offer valuable insights into different growth patterns, revealing fascinating secrets about the world around us.
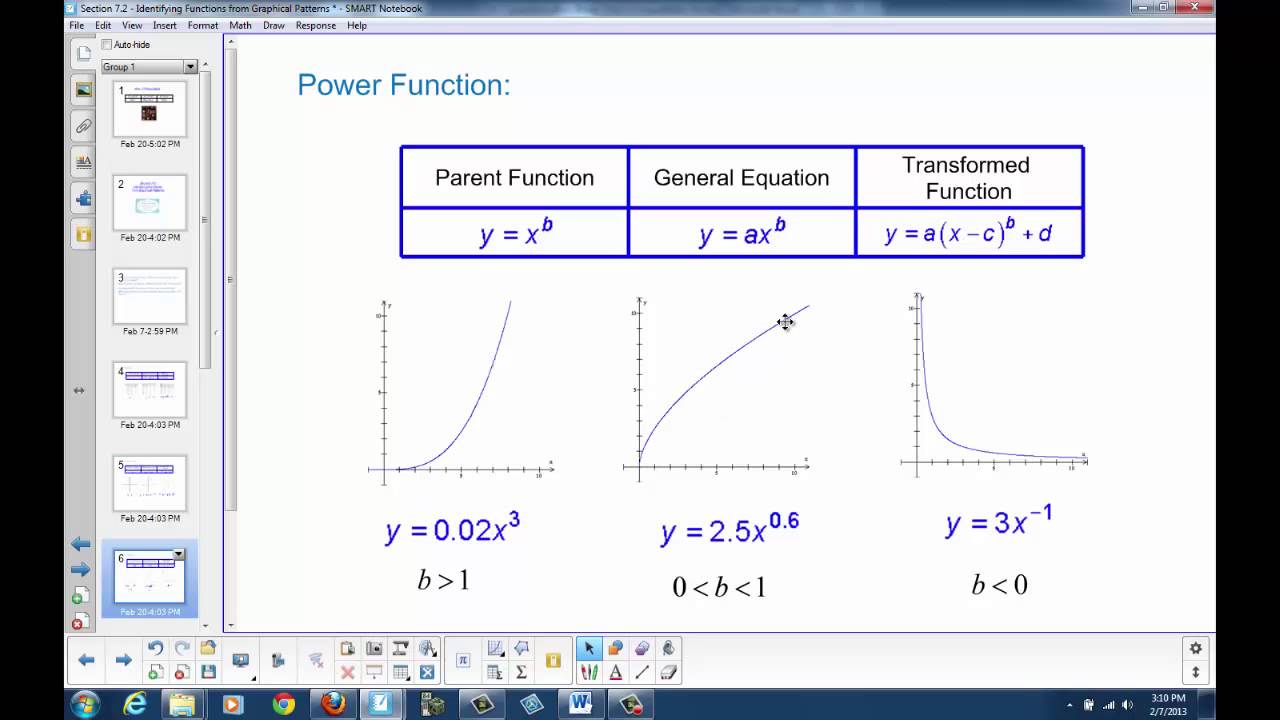
Image: www.youtube.com
Understanding the nuances of quadratic and exponential growth allows us to predict population trends, model the spread of diseases, analyze financial investments, and even comprehend the vastness of the universe. This article delves into the heart of these two fundamental concepts, exploring their unique characteristics, real-world applications, and the compelling differences that set them apart.
Delving into the World of Quadratics
Quadratic Functions: A Tale of Curves
Imagine throwing a ball straight up in the air. The ball follows a graceful arc, rising and then falling back down to Earth. This iconic trajectory is captured by a quadratic function, a mathematical expression that takes the form of y = ax² + bx + c. In this equation, ‘x‘ represents the time, and ‘y‘ represents the ball’s height, while ‘a‘, ‘b‘, and ‘c‘ are constants that determine the specific shape of the curve.
Quadratic functions manifest themselves in various forms beyond ball trajectories. For instance, the area of a square can be expressed as a quadratic function of its side length. Similarly, the profit earned by a company based on the number of units sold can often be modeled using a quadratic equation.
Quadratic Growth: A Steady Pace
Unlike its exponential counterpart, quadratic growth is characterized by a steady, predictable increase. Think of it as a car gradually accelerating on a highway. As time goes on, the car’s speed steadily increases, but the rate of increase remains consistent. This is reflected in the shape of a quadratic graph, which is a symmetrical parabola that opens either up or down, depending on the value of ‘a‘.
The gradual, consistent nature of quadratic growth makes it useful for modeling situations where there is a predictable relationship between two variables. Engineers use it to design bridges and calculate the strength of materials, and economists rely on it to understand the relationship between supply and demand. Whether it’s calculating the volume of water filling a tank or the force required to launch a rocket, quadratic growth provides a reliable framework for understanding and predicting real-world phenomena.
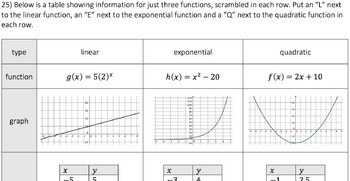
Image: bmp-solo.blogspot.com
Unveiling the Exponential Powerhouse
Exponential Functions: A Leap into the Unknown
While quadratic functions paint a picture of gradual growth, exponential functions are a story of explosive expansion. Imagine a single bacterium dividing into two, each of which then divides again, creating a cascade of progeny that doubles in size with every passing generation. This dramatic increase is the essence of exponential growth, represented by the equation y = abˣ . Here, ‘b‘ is the base, representing the factor by which the quantity grows with each unit of time ‘x‘, and ‘a‘ is the initial value.
Exponential growth is like a rocket taking off, accelerating at an ever-increasing rate. It’s evident in the rapid spread of viral infections, the growth of compound interest, and even in the vastness of the universe. It is a force that can drive innovation, reshape economies, and fundamentally alter the course of history.
Exponential Growth: The Power of Compounding
The defining feature of exponential growth is its accelerating nature. The more time passes, the faster the rate of increase becomes. It’s like a snowball rolling downhill – the bigger it gets, the faster it grows. This compounding effect is why even a modest initial investment can grow into a substantial fortune over time, and why a seemingly harmless virus can quickly escalate into a global pandemic.
Exponential functions are widely employed in various fields. Biologists use them to model population growth, financial analysts use them to project investment returns, and physicists use them to describe radioactive decay and the expansion of the universe. The impact of exponential growth is so profound that it has led to the creation of new disciplines like computational biology and financial engineering.
The Battle of the Giants: Quadratic vs. Exponential
A Tale of Two Growth Patterns
While quadratic growth is characterized by a steady increase, exponential growth exhibits an ever-accelerating growth rate. This fundamental difference sets them apart, making them suitable for modeling different types of phenomena. Imagine painting a picture – quadratic growth might represent the slow and steady progress of filling in the details, while exponential growth would be the dramatic brushstrokes that quickly capture the essence of the scene.
Real-World Applications
To illustrate the practical applications of each growth model, let’s consider two familiar examples:
- Population Growth: While the population of a small village might grow at a relatively constant rate, modeled by a quadratic function, the growth of a global megacity could be better represented by an exponential function, showcasing the rapid increase in inhabitants.
- Investment Returns: A fixed deposit scheme in a bank might offer a modest, consistent interest rate that can be modeled using a quadratic function. In contrast, the growth of a stock market investment, driven by compounding returns, is better suited to an exponential model.
The Importance of Context
Choosing the appropriate growth model is crucial for accurate representation and prediction. In the case of population growth, a quadratic model might be sufficient for short-term predictions, but an exponential model would be necessary for long-term projections. Similarly, for financial investments, a quadratic model might be suitable for analyzing short-term trends, but an exponential model would be more effective for long-term investment planning. The choice of model depends on the specific context and the desired level of accuracy.
Implications and Applications
The understanding of quadratic and exponential growth has profound implications for various fields:
- Economics: Economists use these models to analyze economic growth, inflation, and the effects of government policies.
- Finance: Investors utilize these models to project investment returns, assess risk, and develop investment strategies.
- Biology: Biologists employ these models to study population growth, disease spread, and the evolution of life forms.
- Physics: Physicists use these models to describe phenomena like radioactive decay, gravitational pull, and the expansion of the universe.
Quadratic Vs Exponential
Conclusion
From the subtle curves of quadratic growth to the explosive power of exponential growth, these mathematical models provide a powerful framework for understanding and predicting the ever-changing world around us. By grasping the nuances of each model, we can make informed decisions, solve complex problems, and embark on a journey of discovery to unravel the secrets of growth that shape our world.
The world is full of fascinating examples of quadratic and exponential growth, from the intricate patterns of a flower petal to the overwhelming power of a pandemic. We encourage you to explore these concepts further, apply them to real-world situations, and appreciate the sheer elegance and significance of these fundamental mathematical principles.






