You’ve probably seen those beautiful, symmetrical 3D shapes formed by rotating curves around an axis in calculus class. But have you ever wondered how we calculate the volume of such objects? Enter the disk and washer methods, two powerful tools in calculus that allow us to tackle complex volumes with relative ease. I remember when I first encountered these methods – I was overwhelmed by all the formulas and diagrams. But, after some practice, I realised that they were much simpler than I initially thought, and that was a really satisfying feeling.
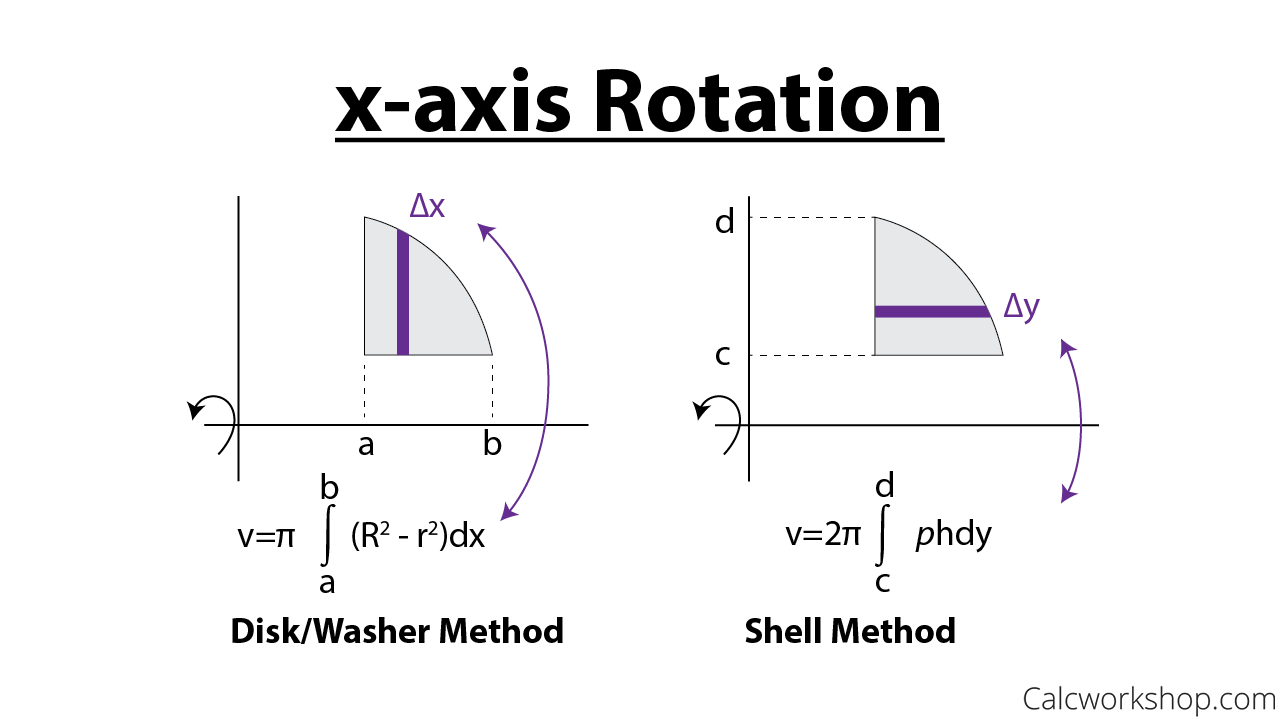
Image: imaginedirectioneramoosmeninos.blogspot.com
Today, we’re going to delve into the world of the disk and washer methods, uncovering their nuances and comparing their applications. By the end, you’ll be able to confidently choose the right method for any given volume problem. Let’s explore these fascinating tools and unlock the secrets of calculating volumes in a whole new way.
Understanding the Foundations: Disks and Washers
The Disk Method:
Imagine a solid object formed by rotating a curve around an axis, a bit like spinning a pizza dough to form a circular crust. The disk method utilizes this analogy by slicing the solid into infinitesimally thin disks – think of them as tiny coins stacked on top of each other. Each disk’s volume is calculated by taking the area of its circular cross-section and multiplying it by its infinitesimal thickness. Summing up the volumes of all these infinitesimally thin disks gives us the total volume of the solid.
Formally, the volume of a solid generated by rotating a function f(x) between x = a and x = b around the x-axis is calculated using the formula:
V = π ∫ab [f(x)]2 dx
The disk method is usually applied when the region being rotated forms a solid with no holes or gaps in the middle.
The Washer Method:
Now, let’s introduce the washer method. It’s like the disk method, but it handles solids with holes. Imagine a donut, where the inside hole is a circular void. We can still use the slicing technique, but our slices will now be washers, with a central hole. To get the volume of each washer, we first calculate the area of the outer circle, then subtract the area of the inner circle, and finally multiply this difference by the washer’s thickness.
To calculate the volume of a solid of revolution with a hole using the washer method, we need to consider two functions: f(x) and g(x). The outer radius of the washer is determined by f(x), while the inner radius is determined by g(x). The volume formula for the washer method is:
V = π ∫ab [f(x)]2 – [g(x)]2 dx
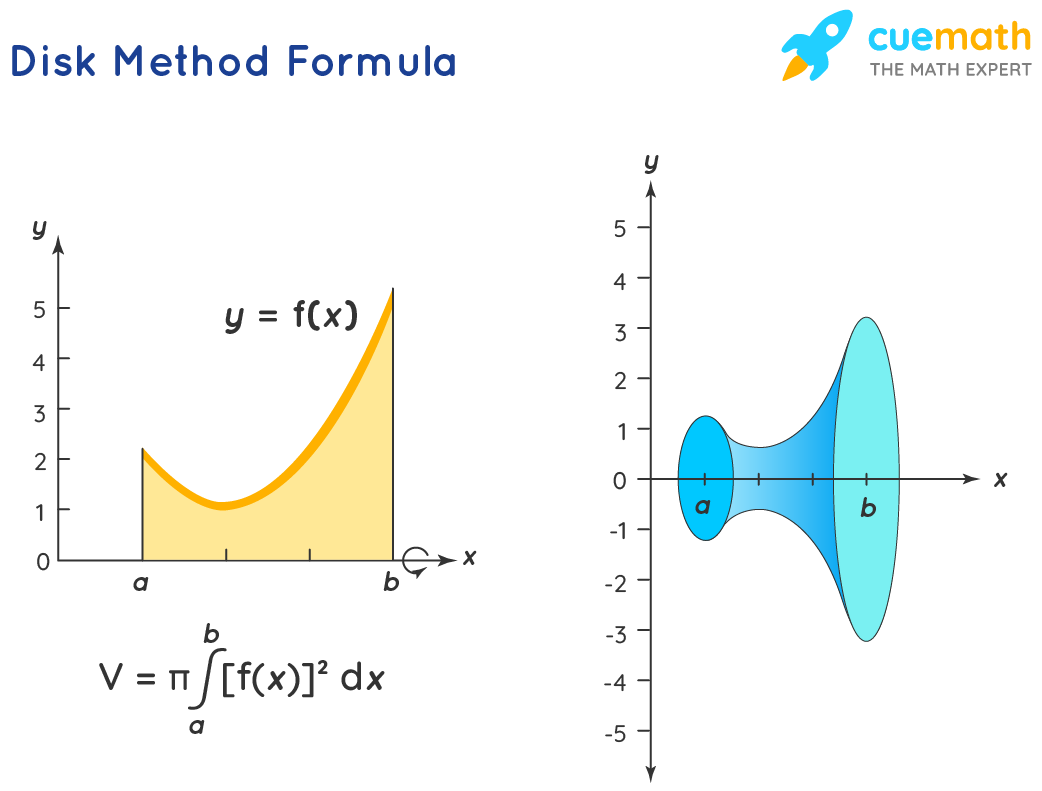
Image: aliarnn.blogfa.com
Disks vs Washers: A Comparative Look
The key difference between the disk and washer methods lies in the shape of the generated solid. The disk method is used for solids with no holes (think of a cylinder or a sphere), while the washer method tackles solids with holes (for example, a donut or a hollow cylinder).
To illustrate this further, imagine a function f(x) that you want to rotate around the x-axis. If the curve is completely above the x-axis, you can apply the disk method. However, if a second function g(x) lies below f(x) and both are rotated around the x-axis, the resulting solid will have a hole in the middle, requiring the use of the washer method.
The core idea behind both methods remains the same: we break down the solid into infinitesimally thin slices. The difference lies in the shape of these slices; they are disks for solids without holes and washers for solids with holes.
Practical Applications of the Disk and Washer Methods
The beauty of these methods lies in their versatility. They are not just theoretical tools but are widely used in real-world applications. Engineers use them to calculate the volume of complex shapes, like airplane wings or turbine blades, which helps them design and analyze these structures. Mathematicians apply them to solve intricate problems in fluid dynamics and other advanced fields.
Imagine a tank with a unique shape. To figure out its capacity, we can employ the disk or washer method by considering its cross-sectional area and integrating it over its height. Similar calculations help determine the volume of intricate medical instruments like artificial heart valves or implants, ensuring they are the right size and shape for their intended purpose.
Expert Tips for Mastering the Disk and Washer Methods
Here are some tips from my experience that will help you excel in using the disk and washer methods:
- Visualize: Before setting up the integral, draw a rough sketch of the solid. Understanding the shape of the solid will help you identify the appropriate method and the radius of the disk or washer.
- Choose the right axis: Sometimes, rotating the curve around a different axis can simplify the problem. Think about which axis would lead to a simpler or more convenient expression for the radius of the disk or washer.
- Don’t forget the thickness: The thickness of the disk or washer is crucial for calculating its volume. In most cases, the thickness is represented by dx or dy depending on the axis of rotation.
- Practice, practice, practice: Like any calculus concept, mastery comes with practice. Try solving different problems with various functions and different axes of rotation. Remember, practice makes perfect.
FAQs: Clearing Up Common Questions
Here are some frequently asked questions about the disk and washer methods:
Q: When do I need to use the washer method instead of the disk method?
A: The washer method is essential when there is a hole (or gap) in the solid of revolution. For a solid with no holes, the disk method is sufficient.
Q: Is it always necessary to rotate around the x-axis?
A: No, you can rotate around the y-axis as well. In this case, the formulas will be slightly modified. You’ll be integrating with respect to y, and the radius of the disk or washer will be expressed in terms of y.
Q: How do I determine the limits of integration?
A: The limits of integration are determined by the points where the function intersects the axis of rotation. For example, if you’re rotating around the x-axis, the limits of integration will be the x-values where the curve intersects the x-axis.
Q: Can I use the disk and washer methods for other shapes besides solids of revolution?
A: While the disk and washer methods are primarily used for solids of revolution, they can be adapted to calculate volumes of other shapes. The key is to break the shape down into infinitesimally thin slices and integrate the volumes of these slices.
Difference Between Disk And Washer Method
Conclusion: Embracing the Disk and Washer Methods
The disk and washer methods are powerful tools that allow us to calculate the volumes of complex shapes via integration. Understanding these methods, with their unique formulas and applications, unlocks a deeper understanding of calculus. It allows us to approach complex volume problems with confidence and precision, making for a more enjoyable and enriching learning experience.
Are you ready to delve deeper into the world of volumes? Are there any specific challenges that you encounter when applying these methods? Share your questions and experiences in the comments below! I’m eager to hear from fellow calculus enthusiasts and share my knowledge.






