Have you ever found yourself staring at a complex 3D shape, wondering how to calculate its volume? The answer might just lie in two powerful methods: the washer and disk methods. These techniques, rooted in calculus, allow us to break down complicated shapes into simpler, manageable pieces, making volume calculations a breeze.

Image: officialbruinsshop.com
Imagine you’re baking a layered cake. Each slice represents a cross-section of the cake, and knowing the area of that slice allows you to determine the total volume. The washer and disk methods work similarly, using slices to approximate the volume of 3D objects.
Understanding the Washer and Disk Methods
Both the washer and disk methods are based on the principle of slicing a solid into infinitesimally thin cross-sections. We then calculate the area of each slice and integrate over the entire solid to find the total volume.
The Disk Method: A Slice of Simplicity
The disk method is applied to solids that are generated by revolving a region around a single axis. Essentially, you’re taking a 2D shape and rotating it to create a 3D form. Think of a circular pizza slice spinning about its center – this would create a cone!
To use the disk method, envision a slice of your solid as a thin disk. The area of each disk is simply the area of a circle (πr²), where ‘r’ is the radius of the slice. By integrating this area across the entire solid’s height, we obtain the total volume.
The Washer Method: Adding a Hole
Now, imagine you’re making a doughnut by rotating a ring-shaped region around an axis. This solid has a hole in its center. Here, the washer method comes into play.
The washer method is used for solids with a hole. It is very similar to the disk method, however, we now consider the difference between the outer radius (R) and the inner radius (r) of each washer. The area of each washer is then π(R² – r²), and we integrate this difference in area over the entire solid to find the total volume.
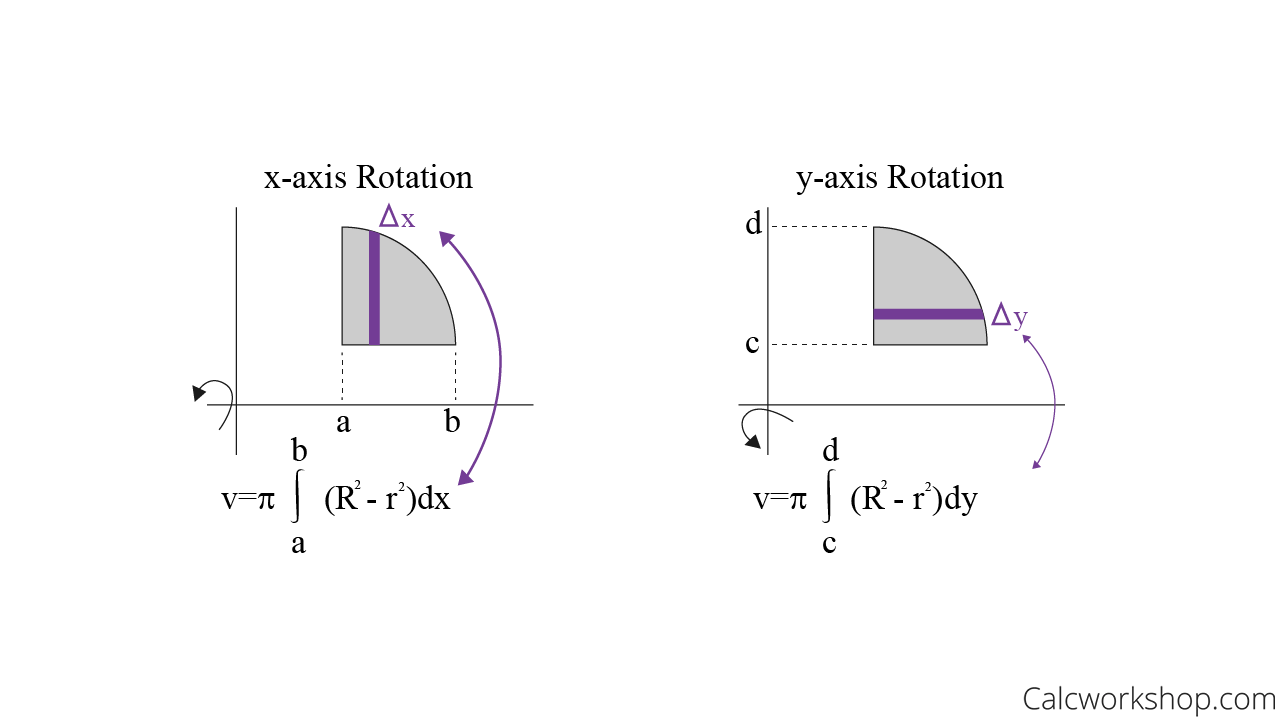
Image: officialbruinsshop.com
When to Use Which Method?
Choosing between the washer and disk method depends on the shape of your solid.
Use the disk method when:
- The solid is generated by revolving a region around an axis and it has no hole.
- The cross-section is a simple shape, such as a circle or square.
Use the washer method when:
- The solid is generated by revolving a region around an axis but has a hole.
- The cross-section resembles a washer or ring.
Examples: Visualizing the Methods
Example 1: Disk Method – Finding the Volume of a Cone
Imagine rotating a right triangle around one of its legs. This generates a cone. To calculate its volume using the disk method, we would first consider the radius of each disk as a function of its height. Then, we would integrate the area of each disk (πr²) over the height of the cone to obtain its volume.
Example 2: Washer Method – Finding the Volume of a Doughnut
Take a ring-shaped region and rotate it around its center. This generates a doughnut. To calculate its volume using the washer method, we would determine the outer radius (R) and inner radius (r) of each washer, then integrate the area of each washer (π(R² – r²)) over the entire height of the doughnut to obtain its volume.
Tips and Expert Advice
Here are some tips for mastering the washer and disk methods:
- Sketch the Solid: Visualize the solid being formed. This helps you determine the radius and limits of integration.
- Break it Down: Divide the solid into thin slices (disks or washers) and express their area in terms of the variable of integration.
- Set Up the Integral: Write an integral representing the sum of the areas of all the slices.
- Evaluate the Integral: Use the fundamental theorem of calculus to calculate the definite integral and obtain the total volume.
Remember, the washer and disk methods are powerful tools for finding the volumes of complex shapes. The key is understanding the principle behind them and practicing their application.
FAQ
Q: What if the solid has a more complex cross-section, like a rectangle?
A: You can still apply the washer and disk methods, but you’ll need to adjust the formula for the area of the cross-section accordingly. For a rectangular cross-section, the area would be length times width.
Q: How do I choose the limits of integration?
A: The limits of integration are the values of the variable that define the start and end of your solid. Look at the shape and determine the values where your slices begin and end.
Q: Are there other methods for calculating volumes besides the washer and disk methods?
A: Yes, there are other methods like the shell method. However, the washer and disk methods are often easier to visualize and apply, especially for most standard shapes.
Washer Method Vs Disk Method
https://youtube.com/watch?v=7c6ZWUxL-wo
Conclusion
The washer and disk methods are indispensable tools for calculating volumes of solids of revolution. By understanding the concepts behind them and practicing their application, you can confidently tackle complex volume problems.
So, are you ready to dive deeper into the intricate world of volume calculations? Let us know in the comments below if you have any questions or would like to explore further!






