Imagine yourself standing at the center of a bustling roundabout. Cars whiz by, each taking a circular path around you. Have you ever wondered how the distance around each car’s path relates to its size? This seemingly simple question leads us to a fundamental concept in mathematics: the **radius** and its connection to **pi**, a transcendental number that plays a crucial role in understanding circles.
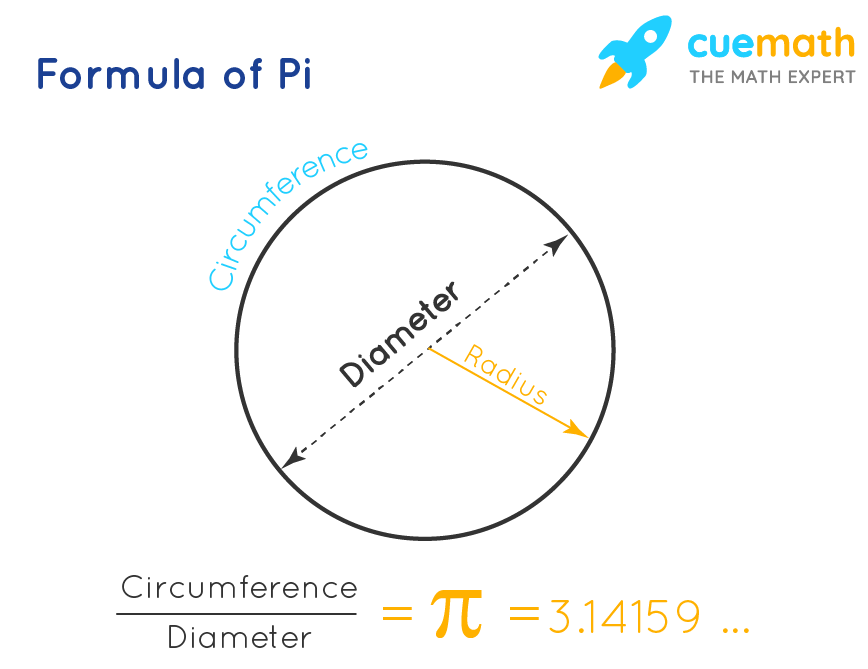
Image: www.cuemath.com
In this article, we’ll delve deeper into the concept of a 2π radius, unraveling its significance in geometry and exploring its applications across various fields. From the ancient mathematicians who first discovered pi to modern-day advancements in technology, the relationship between a circle’s radius and its circumference remains a cornerstone of mathematical understanding.
Understanding 2π Radius
The concept of radius is central to understanding circles. It refers to the distance between a circle’s center and any point on its circumference. In essence, the radius is the “backbone” of a circle, determining its size and shape. When we talk about a 2π radius, we are referring to a circle where the distance from the center to any point on its circumference is 2π.
Why 2π? Because it directly connects the radius to another fundamental property of a circle: its **circumference**. The circumference is the total distance around the circle. A remarkable relationship exists between the radius and circumference, which is expressed by the formula:
Circumference = 2πr
Where “r” represents the radius of the circle. This formula highlights the inherent connection between the circumference and radius via the constant π, approximately equal to 3.14159. Hence, a circle with a 2π radius has a circumference of 2π * 2π, which simplifies to 4π².
The Significance of 2π Radius
The concept of 2π radius is not merely a mathematical curiosity; it holds profound implications in various fields.
Geometry and Trigonometry
In geometry and trigonometry, the 2π radius plays a fundamental role in understanding the properties of circles. It helps define the relationship between the radius, diameter, circumference, and area of a circle. The constant π, intertwined with the radius, enables us to calculate these essential properties with precision.

Image: allyntremblay1954.blogspot.com
Engineering and Physics
Engineers and physicists leverage the principles of 2π radius in numerous applications. The design of wheels, gears, pipes, and other circular objects relies on these fundamental geometric principles. For example, in fluid dynamics, the 2π radius serves as a crucial parameter in understanding the flow of liquids and gases through pipes.
Astronomy and Cosmology
Looking beyond Earth, astronomers and cosmologists utilize the concept of 2π radius in their studies of celestial bodies. Planetary orbits, the motion of stars, and the formation of galaxies all involve circular or elliptical paths, and the understanding of radii and their relation to circumference is crucial in modeling and analyzing these celestial phenomena.
The Latest Trends and Developments
The study of circles and pi continues to evolve, driven by advancements in technology and the pursuit of ever-increasing precision. Research into the properties of pi has yielded remarkable breakthroughs, leading to new algorithms for calculating its value to an unprecedented number of decimal places.
Recent developments in computing power have made it possible to determine pi to trillions of digits. This remarkable achievement has implications beyond just mathematical curiosity. It fuels advancements in cryptography, Monte Carlo simulations, and other fields where precise calculations are indispensable.
The study of 2π radius and its connection to pi remains an active area of research. Scientists are exploring the potential for applications in fields as diverse as quantum mechanics, materials science, and even the study of consciousness.
Tips and Expert Advice
Whether you are a student studying geometry, an engineer designing a circular structure, or simply someone fascinated by the wonders of mathematics, understanding the 2π radius offers valuable insights.
Here are some tips to deepen your understanding and appreciation of this concept:
- Visualize: Draw circles of different radii and calculate their circumferences. Seeing the relationship between the radius and circumference visually reinforces the mathematical principles.
- Explore Resources: There are numerous online resources and books that delve into the fascinating history and applications of pi. Explore these resources to broaden your understanding of this fundamental constant.
- Practice Problems: Solve problems involving circles and their radii. Practice helps solidify your theoretical understanding and builds your problem-solving skills.
- Think Beyond the Classroom: Look for circular patterns and shapes in your everyday environment. Consider how the concept of radius and circumference apply to real-world objects and situations.
FAQs on 2π Radius
Q: What is the difference between a 2π radius and a 1π radius?
A: A circle with a 2π radius is twice the size of a circle with a 1π radius. The radius directly determines the size of the circle, and the circumference scales accordingly. A 2π radius circle will have a circumference twice as large as a 1π radius circle.
Q: Why is pi (π) important in calculating the circumference of a circle?
A: Pi represents the ratio of a circle’s circumference to its diameter. It’s a fundamental constant that governs the inherent relationship between a circle’s size and its distance around. This ratio is consistent for all circles, regardless of their size.
Q: Is there a limit to how many decimal places pi can be calculated to?
A: Pi is an irrational number, meaning it has an infinite number of decimal places that never repeat. While we cannot calculate pi to an infinite number of decimal places, advancements in computing power allow us to determine trillions of digits, providing a level of precision sufficient for most practical applications.
2 Pi Radius
Conclusion
The 2π radius, a seemingly simple concept, unlocks a world of mathematical elegance and practicality. From the basic properties of circles to complex applications in engineering, astronomy, and beyond, the relationship between a circle’s radius and its circumference continues to fascinate and inspire.
Understanding the 2π radius empowers us to appreciate the beauty and interconnectedness of mathematics and its relevance to our world. Are you interested in further exploring the fascinating world of circles and pi?






