Remember those tricky calculus problems in high school? The ones with the confusing notation like “dx/dy” or “dy/dx”? I certainly did! It felt like a secret code only mathematicians understood. But let me tell you, once you grasp the meaning behind these symbols, calculus becomes a fascinating journey into the world of rates of change, slopes, and the very essence of how things evolve. This article will demystify this seemingly complex concept, revealing its simplicity and importance.

Image: barkmanoil.com
In this article, we’ll explore what dx/dy and dy/dx represent, their roles in calculus, and how they help us understand the world around us. We’ll also delve into some of the latest trends in calculus and offer tips for mastering this fundamental mathematical tool.
Understanding the Essence of dx/dy and dy/dx
At its core, dx/dy and dy/dx are not just random symbols, but powerful tools for representing rates of change. They form the basis of differential calculus, a branch of mathematics that deals with the study of continuous change.
Imagine a car traveling down a road. Its position changes over time, and we can express this change using a function. If we plot the car’s position on a graph, the slope of the line at any given point represents the car’s velocity – how fast it is moving at that instant. That’s where dx/dy or dy/dx come into play. They tell us how much the dependent variable (y) changes for a given change in the independent variable (x).
Delving Deeper: A Clear Explanation of dx/dy and dy/dx
To grasp the concept fully, let’s break down these symbols individually:
dy/dx – Deriving the Rate of Change
The most common notation, dy/dx, represents the derivative of a function y with respect to x. In simpler terms, it tells us how much the value of y changes for every unit change in the value of x. It’s like asking “How fast is y changing when x changes?”.
Think of it as the slope of the line tangent to the function’s graph at a particular point. Calculating dy/dx gives us a precise way of measuring the instantaneous rate of change of a function. This is crucial in many real-world applications, from calculating the speed of a moving object to analyzing stock market trends.
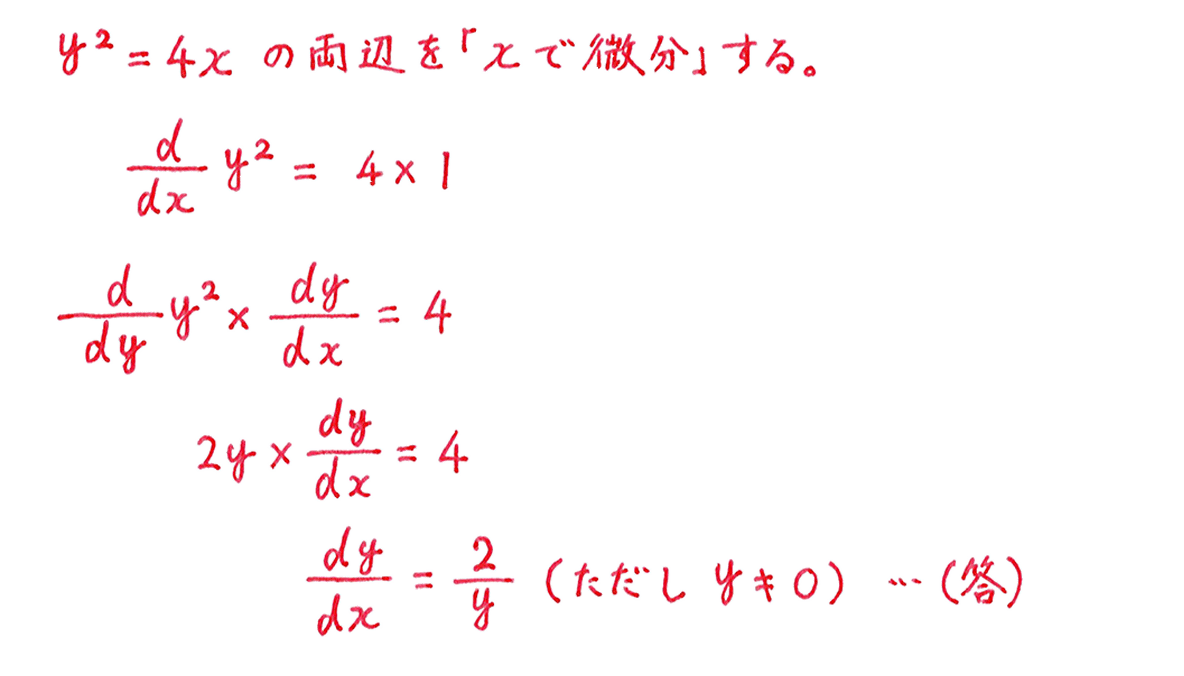
Image: www.try-it.jp
dx/dy – Flipping the Perspective
dx/dy is simply the reciprocal of dy/dx. It essentially inverts the perspective and asks how much x changes for every unit change in y. In other words, it’s like asking, “How much does x change when y changes?”
Imagine a scenario where you want to know how the volume of a sphere changes with respect to its radius. Using dx/dy, we can determine how much the radius needs to change for a given change in volume. This perspective can be especially useful when you want to understand the relationship between two quantities where one is directly dependent on the other.
The Significance of dx/dy and dy/dx in Real-World Scenarios
The concepts of dx/dy or dy/dx are not just mathematical curiosities. They are fundamental tools for understanding a wide range of real-world phenomena:
- Physics: Calculating the acceleration of a moving object, determining the speed of a projectile, and even understanding the force of gravity all involve derivatives.
- Engineering: Analyzing the stress and strain on a bridge, optimizing the design of an airplane wing, and understanding the flow of fluids in a pipe all rely on calculus concepts.
- Economics: Predicting market trends, analyzing economic growth, and understanding consumer behavior often utilize derivatives to calculate marginal cost, marginal revenue, and other important economic factors.
- Biology: Studying population growth, analyzing enzyme kinetics, and modeling disease spread all heavily rely on calculus techniques.
Latest Trends and Developments in Calculus
The field of calculus is constantly evolving, with new discoveries and advances reshaping our understanding of continuous change. Here are some of the recent trends:
- Fractional Calculus: Traditionally, calculus deals with derivatives and integrals of whole orders. But fractional calculus explores derivatives and integrals of non-integer orders, leading to new ways of modeling complex phenomena like diffusion and viscoelasticity.
- Geometric Calculus: Focusing on geometric applications of calculus, this area introduces new tools for studying curves, surfaces, and complex shapes, with applications in computer graphics, robotics, and even medical imaging.
- Computational Calculus: With the advent of powerful computing tools, computational calculus has emerged, allowing for the numerical solution of complex differential equations, which are often impossible to solve analytically. This opens up doors to modeling systems more realistically and understanding real-world processes with greater accuracy.
Expert Tips for Mastering Calculus
If you’re struggling to grasp the concepts of dx/dy or dy/dx, keep in mind that practice is key. Here are some tips to help you on your calculus journey:
- Start with the basics: Make sure you have a strong foundation in algebra and pre-calculus before diving into derivatives and integrals.
- Visualize the concepts: Don’t just memorize formulas. Try to visualize what the derivative or integral represents graphically, using examples like motion and distance.
- Practice problem solving: Start with simple problems and gradually work your way up to more challenging ones. The more problems you solve, the better your understanding will become.
- Seek help when needed: Don’t be afraid to ask for help from your teacher, tutor, or online resources when you encounter difficulties.
FAQs about dx/dy and dy/dx
Here are some frequently asked questions about dx/dy and dy/dx:
What is the difference between dx/dy and dy/dx?
dx/dy is the reciprocal of dy/dx. They represent different perspectives on the rate of change. dy/dx tells us how y changes with respect to x, while dx/dy tells us how x changes with respect to y.
Why are dx/dy and dy/dx important in calculus?
They are the fundamental building blocks of differential calculus, allowing us to study and analyze continuous change. They are essential for understanding rates of change, slopes, and the behavior of functions.
Can I use dx/dy and dy/dx in real-world applications?
Absolutely! They are crucial for understanding a wide range of phenomena in physics, engineering, economics, biology, and more.
Are dx/dy and dy/dx related to integration?
Yes, they are closely related to integration. Integration is the inverse operation of differentiation. If you know the derivative of a function, you can use integration to find the original function.
Dx/Dy Or Dy/Dx
Conclusion: Unveiling the World of Continuous Change
The symbols dx/dy and dy/dx may seem daunting at first, but they represent a powerful and elegant concept that allows us to understand the world of continuous change. From calculating the speed of a falling object to modeling the growth of a population, these seemingly simple symbols are at the heart of some of the most profound scientific discoveries.
Are you ready to delve deeper into the fascinating world of calculus and explore the potential of dx/dy and dy/dx? Share your thoughts and questions in the comments below, and let’s continue this exciting exploration together!






