Have you ever wondered what happens when you split a dozen cookies evenly among four friends? This simple question leads us to the fascinating world of division, a fundamental concept in mathematics. Today, we’re diving deep into the intricacies of 12 divided by 4, exploring its history, practical applications, and how it connects to the very essence of numbers.
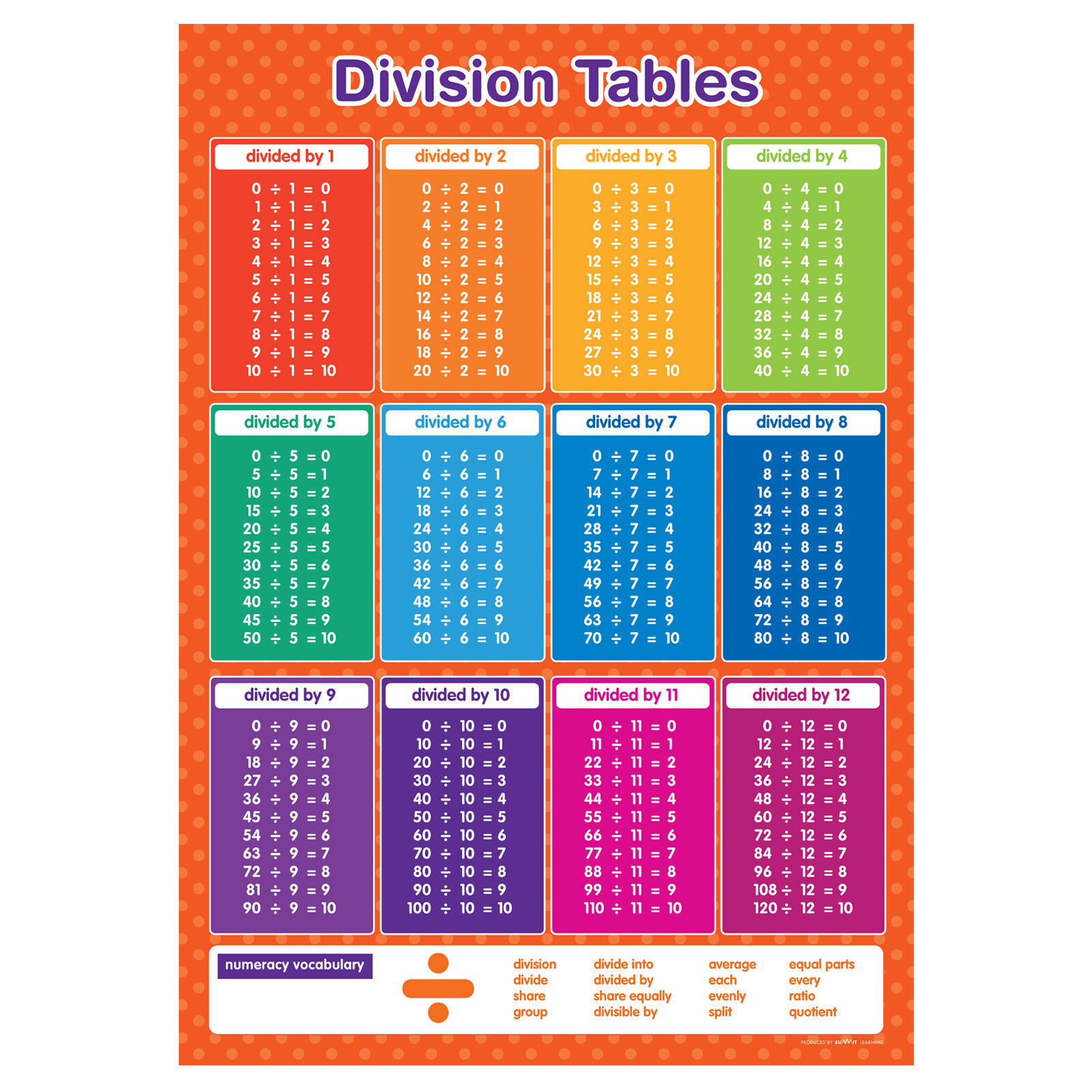
Image: www.veteransinstem.org
Dividing 12 by 4 might seem like a straightforward calculation, but beneath its surface lies a world of mathematical beauty. It’s a stepping stone to understanding more complex arithmetic, vital for everyday tasks like budgeting, cooking, and even understanding the mechanics of our world.
The Journey Begins: What is Division?
In its simplest form, division is the process of splitting a whole into equal parts. When we divide 12 by 4, we’re asking: “How many groups of 4 can we make from 12?” The answer, as we’ll discover, is 3.
Understanding the Components: Dividend, Divisor, and Quotient
Before we jump into the calculation, let’s introduce the key players:
- Dividend: The number being divided (in our case, 12)
- Divisor: The number we’re dividing by (in our case, 4)
- Quotient: The result of the division (in our case, 3)
The Magic of Calculation: 12 Divided by 4
Now let’s tackle the main event: 12 divided by 4. There are various ways to approach this, each illustrating different facets of division:
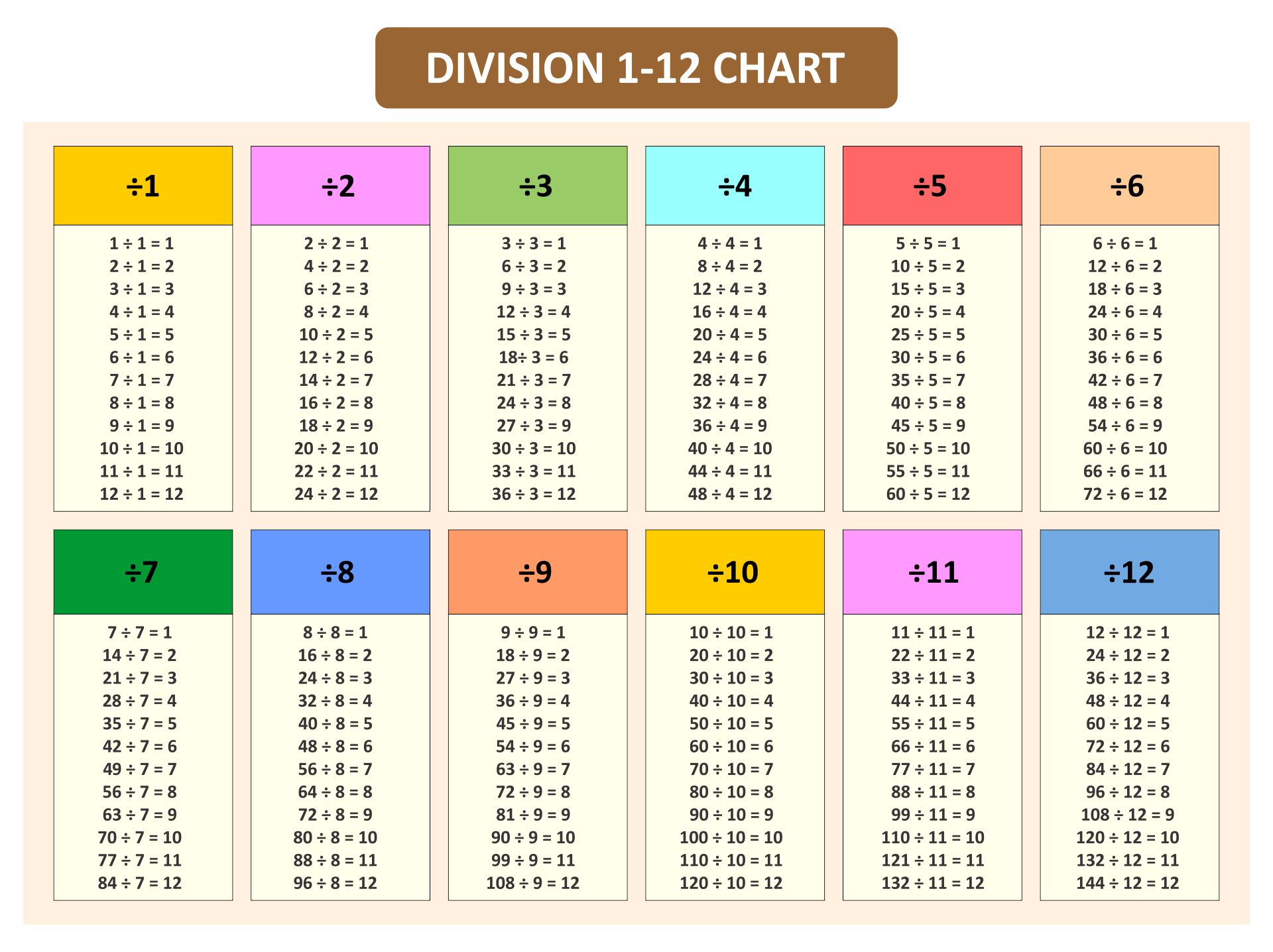
Image: dl-uk.apowersoft.com
1. Visual Representation
Imagine 12 cookies arranged in rows. To divide them by 4, we group them into sets of 4. We’ll end up with 3 groups of cookies, representing the quotient of 3.
2. Repeated Subtraction
We can start with 12 and repeatedly subtract 4 until we reach 0. We can subtract 4 three times, which again signifies the quotient of 3.
3. Long Division
This method, though slightly more complex, is crucial for understanding larger divisions. We set up the problem like this:
3
4|12
12
---
0We find the largest number that can be multiplied by 4 and still be less than or equal to 12 (which is 3), write it above the line, and then subtract 12 from 12. Our remainder is 0, confirming that 12 divided by 4 is 3.
Real-World Applications: More Than Just Cookies
Beyond cookie-sharing, division plays a crucial role in everyday life:
1. Budgeting
Dividing your monthly income by the number of weeks in a month helps you determine your weekly budget, allowing for better financial planning.
2. Cooking
Recipes often require adjustments based on the number of servings. Dividing ingredients by a scaling factor ensures accurate measurements.
3. Engineering
Engineers utilize division to calculate load distribution in structures, ensuring safety and stability.
4. Measurement
Dividing lengths, areas, or volumes is essential for converting units, such as converting meters to inches or gallons to liters.
Beyond the Basics: Exploring Multiplication’s Role
Division and multiplication are inextricably linked. Dividing 12 by 4 is equivalent to finding a number that, when multiplied by 4, equals 12. In this case, that number is 3.
Historical Insights: Division Through the Ages
Division has been a fundamental tool for humanity since the dawn of civilization. Ancient civilizations like the Babylonians and Egyptians used sophisticated methods to divide numbers, laying the foundation for the mathematics we use today.
The Future of Division: Advances in Computation
With the advent of computers, division has become even more powerful. Computer algorithms can handle complex calculations involving massive numbers, allowing us to explore new frontiers in science, engineering, and finance.
The Importance of Understanding Division
Understanding division is crucial for navigating the complexities of our world. Mastering this simple concept empowers you to make informed decisions, solve problems, and engage with the world around you in a more meaningful way.
12 Divided By 4
Conclusion
From splitting cookies to constructing bridges, division is a fundamental concept with a profound impact on our lives. We’ve explored its basics, applications, and historical significance, demonstrating its importance in both everyday tasks and scientific advancements. So next time you encounter a division problem, remember that beneath its surface lies a universe of mathematical beauty and practical utility.






