Have you ever been caught off guard by a simple percentage question? Imagine you’re at the grocery store, and you see a sale on your favorite brand of cereal. The box is marked “15% off,” but it’s originally priced at $6. You try to quickly figure out how much you’ll save, but the percentage calculation seems daunting. That’s where understanding “what percent of 60 is 15” comes in handy. This seemingly straightforward question opens a door to understanding proportions and percentages, which are essential in various aspects of our lives.

Image: www.researchgate.net
Knowing how to calculate percentages and figure out proportions can save you money, help you make informed decisions, and even impress your friends with your quick mental math skills. In this guide, we’ll delve into the world of percentages, break down the steps to calculate “what percent of 60 is 15,” and provide helpful tips to make these calculations a breeze.
Understanding Percentages and Proportions
Percentages are a convenient way to express a part of a whole. The word “percent” literally means “out of one hundred,” which is why they’re represented by the symbol “%.” When we say “what percent of 60 is 15,” we’re essentially asking what portion of 60 does 15 represent, expressed as a fraction of 100.
Understanding proportions is key to solving percentage problems. A proportion is a statement of equality between two ratios. In our case, we have the ratio 15/60, representing the part (15) compared to the whole (60). We want to find the equivalent ratio that expresses this proportion as a percentage, meaning its denominator is 100, which we’ll represent as x/100.
Finding the Solution
Setting Up the Equation:
To solve “what percent of 60 is 15,” we set up a simple equation:
15 / 60 = x / 100
This equation states that the ratio of 15 to 60 is equivalent to the ratio of x to 100. Now we need to solve for x, which will give us the percentage.
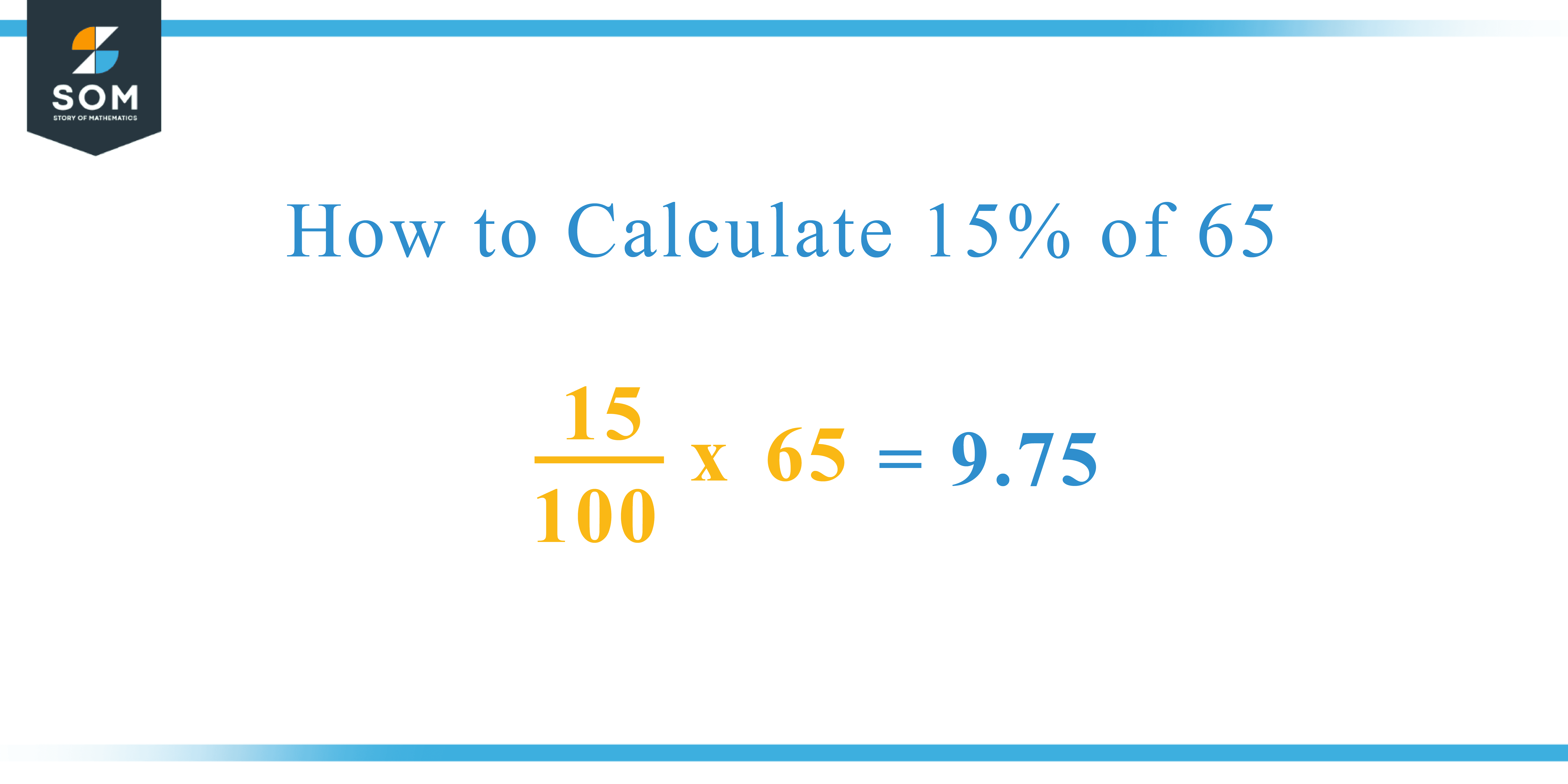
Image: www.storyofmathematics.com
Cross-Multiplication:
To solve for x, we use cross-multiplication. This means multiplying the numerator of one ratio by the denominator of the other ratio and setting the products equal to each other.
15 * 100 = 60 * x
Simplifying this equation, we get:
1500 = 60x
Solving for x:
To isolate x, we divide both sides of the equation by 60:
1500 / 60 = 60x / 60
This gives us:
x = 25
Therefore, 15 is 25% of 60.
Real-World Applications
The application of percentage calculations isn’t limited to grocery store sales. These skills are invaluable in various aspects of our daily lives:
- Finance: Calculating interest rates, loan payments, and investment returns.
- Shopping: Determining discounts, sales tax, and comparing prices.
- Healthcare: Understanding medication dosages and analyzing health data.
- Science: Expressing experimental data, determining concentrations, and interpreting scientific results.
Tips and Expert Advice
Here are some expert tips to make calculating percentages easier:
- Use a Calculator: Even if you can perform mental math, a calculator can be helpful for complex percentages.
- Fractions & Decimals: Understand the relationship between fractions, decimals, and percentages. Remember that 1/2 is equal to 0.5 and 50%.
- Practice: The more you practice, the more comfortable you’ll become with calculating percentages.
- Memorize Common Percentages: Knowing key percentages like 10%, 25%, and 50% can help you estimate quickly.
If you find yourself struggling, remember that online calculators and educational resources are available to help you. Don’t be afraid to seek assistance when needed.
FAQs (Frequently Asked Questions)
Q1: What if I need to calculate a percentage without a calculator?
You can use the “percentage formula”:
Percentage = (Part / Whole) * 100
For example, to find what percentage 15 is of 60, we’d plug in the values:
Percentage = (15 / 60) * 100 = 0.25 * 100 = 25%
Q2: What about calculating the whole when you have the percentage and the part?
You can use the formula:
Whole = (Part / Percentage) * 100
For example, if 25% of a number is 15, we can find the whole number:
Whole = (15 / 25) * 100 = 0.6 * 100 = 60
What Percent Of 60 Is 15
Conclusion
Understanding “what percent of 60 is 15” goes beyond simply finding the answer; it’s about grasping the concepts of percentages, proportions, and how these relate to everyday situations. You can use these skills to make informed decisions, solve problems, and confidently navigate a world filled with percentage-based information.
Are you interested in learning more about percentages and how to apply them in different scenarios? Share your thoughts and questions in the comments below!






