Remember that math test in elementary school where we were first introduced to division? My heart would race whenever I saw problems like “144 divided by 12.” The thought of dividing such large numbers sent shivers down my spine! However, as I learned more about the fundamental principles of division, that fear quickly dissolved, transforming into a sense of understanding and accomplishment. Today, we’ll delve into the world of division, exploring the concept of 144 divided by 12, and unraveling the magic behind this simple but powerful operation.
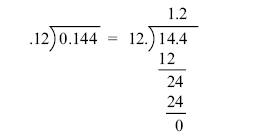
Image: avstop.com
Understanding division is like mastering a magical key that can unlock a treasure chest of knowledge. It’s a universal concept that plays a significant role in our daily lives. From splitting a pizza evenly with friends to calculating the average score on a test, we unknowingly utilize division in various situations. Let’s journey into the realm of 144 divided by 12 and uncover the beauty hidden within this mathematical equation.
Understanding the Basics of Division
Division is an arithmetic operation that involves splitting a whole number into equal parts. It helps us determine how many times a particular number can fit into another number. In our case, we want to find out how many times the number 12 fits into the number 144. We can represent this division problem as: 144 ÷ 12.
The answer to this division problem is 12. In other words, 12 can fit into 144 twelve times. To visualize this, imagine 144 objects arranged in rows – each row containing 12 objects. You’ll find you need exactly 12 rows to accommodate all 144 objects.
The “Long Division” Method
One popular method for solving division problems is called “long division.” This method allows us to systematically divide a larger number by a smaller number. Here’s how it works:
- Write the dividend (144) inside a division bracket and the divisor (12) outside the bracket.
- Ask yourself: How many times does 12 go into 14? The answer is 1. Write 1 above the 4 in the dividend.
- Multiply the divisor (12) by the quotient (1) and write the product (12) below the 14.
- Subtract 12 from 14, leaving 2.
- Bring down the next digit (4) from the dividend, forming 24.
- Repeat steps 2-5 until you reach a remainder of 0. In this case, 12 goes into 24 twice (2 x 12 = 24).
The final quotient above the division bracket is the answer to the division problem. In this case, the quotient is 12, meaning 144 divided by 12 equals 12.
It is important to remember that dividing by 12 is essentially asking “How many groups of 12 can we make from 144?” The answer, as we’ve seen, is 12 groups.
The Importance of Division in Real Life
Division is more than just a mathematical operation; it’s a tool for understanding and solving numerous real-world problems. Think about these scenarios:
- Sharing equally: Imagine you have 144 cookies and want to share them equally among your 12 friends. Simple division (144 ÷ 12) tells you that each friend will get 12 cookies.
- Calculating averages: To calculate the average score on a test, you add up all the scores and then divide the total by the number of students who took the test. For example, if five students score 84, 92, 78, 90, and 86, the average score would be (84 + 92 + 78 + 90 + 86) / 5 = 86.
- Measuring proportions: In cooking, you often need to adjust recipes based on the number of people you’re serving. Division allows you to calculate the correct proportion of ingredients. For example, if a recipe calls for 12 ounces of flour for 4 servings, you can calculate the amount of flour needed for 8 servings by: 12 ounces / 4 servings = 3 ounces per serving. Then you multiply that by the new number of servings: 3 ounces/serving * 8 servings = 24 ounces of flour.
These examples highlight the practicality of division in everyday situations. Its ability to break down quantities, calculate averages, and determine proportions makes it an indispensable tool for navigating our world.
Image: www.numerade.com
Mastering Division: Tips for Success
Mastering division is like any skill – consistency and practice are key. Here are some tips to help you become a division whiz:
- Start with basic facts: Memorizing multiplication tables can greatly enhance your ability to solve division problems. If you know 12 x 12 = 144, you can immediately determine that 144 ÷ 12 = 12.
- Practice regularly: Solve various division problems to develop problem-solving skills and strengthen your understanding of the process.
- Utilize visual aids: Drawing diagrams or using manipulatives can help visualize the concept of division and make it more tangible. For example, try dividing 144 marbles into 12 equal-sized groups.
- Don’t be afraid to make mistakes: Mistakes are part of the learning process. View them as opportunities to review your understanding and refine your approach.
The beauty of division lies in its simplicity and effectiveness. It’s a fundamental tool that empowers us to tackle diverse challenges and make sense of our world. By embracing practice and exploring diverse applications, you can master this essential mathematical concept and unlock a world of possibilities.
Frequently Asked Questions (FAQs) about Division
Q: Is division commutative?
A: No, division is not commutative. This means that the order of the numbers in a division problem does matter. For example, 144 ÷ 12 does not equal 12 ÷ 144.
Q: What happens when the dividend is smaller than the divisor?
A: If the dividend is smaller than the divisor, the quotient will be less than 1. For example, 12 ÷ 144 equals 0.0833.
Q: What is the role of the remainder in division?
A: The remainder represents the part of the dividend that is left over after dividing by the divisor. For example, if we divide 145 by 12, the remainder is 1.
144 Divided By 12
Q: Can division be performed with decimals?
A: Yes, division can be performed with decimals. The process is similar to dividing whole numbers, but requires extra care when aligning decimal points.
Division is a fundamental pillar of mathematics, empowering us to tackle various real-world problems with clarity and understanding. From sharing resources fairly to calculating averages and proportions, division plays a crucial role in shaping our world.
Are you fascinated by the intricate world of division and its applications? Let us know your thoughts and experiences with this essential mathematical operation!






