Remember those frustrating math problems in school where you had to figure out all the numbers that go evenly into another number? I certainly do. One that always seemed to pop up was finding the factors of 196. At first, it seemed like a random assortment of numbers, but as I dug deeper, I realized there was a fascinating logic behind it. This journey of understanding the factors of 196 turned out to be a gateway into the world of prime factorization and divisibility rules – a world filled with hidden patterns and surprising connections.
Image: www.storyofmathematics.com
Today, we’ll explore the factors of 196 in detail, dissecting this seemingly simple concept to uncover its deeper meaning. We’ll delve into the world of prime factorization, learn how to identify factors, and discover practical applications of these concepts in everyday life. By the end of this article, you’ll not only understand the factors of 196, but you’ll also have a solid foundation in the principles that govern divisibility and factorization.
Understanding Factors and Divisibility
Definition and Explanation
In simple terms, factors are the numbers that can divide another number evenly without leaving a remainder. Let’s take the number 12. The factors of 12 are 1, 2, 3, 4, 6, and 12 because they all divide 12 evenly. The concept of factors is closely tied to divisibility. A number is considered “divisible” by another number if it can be divided by that number without leaving a remainder.
Prime Factorization: Deconstructing Numbers
Every whole number above 1 can be expressed as a unique product of prime numbers. This process is known as prime factorization. A prime number is a whole number greater than 1 that is only divisible by 1 and itself. For example, the prime factorization of 12 is 2 x 2 x 3, where 2 and 3 are prime numbers.
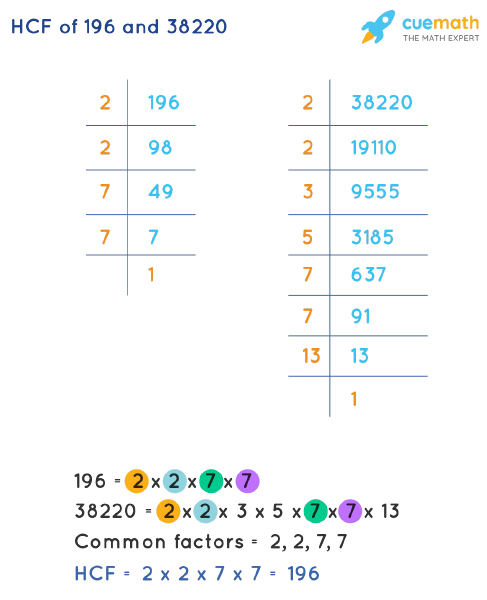
Image: www.cuemath.com
Finding the Factors of 196
Now, let’s get back to 196. To find its factors, we can follow these steps:
- Start by listing the first few numbers that divide 196 evenly. We know 1 and 196 are always factors. We can quickly see that 2 divides 196 evenly (196 / 2 = 98).
- Continue listing pairs of factors. Since 2 is a factor, we can find its corresponding factor by dividing 196 by 2, which gives us 98. So, 2 and 98 are a factor pair.
- Keep checking for factors. Does 3 divide 196 evenly? No, it doesn’t. How about 4? Yes! 196 / 4 = 49, so 4 and 49 are another factor pair.
- Keep going until no more factors are found. We can see that 7 divides 196 evenly (196 / 7 = 28), giving us another pair. Finally, we realize that 14 divides 196 evenly (196 / 14 = 14), giving us a final pair.
Therefore, the factors of 196 are: 1, 2, 4, 7, 14, 28, 49, 98, and 196.
An alternative method for finding factors is through prime factorization. Let’s break 196 down into its prime factors: 196 = 2 x 2 x 7 x 7 = 22 x 72. To list all the factors, we use combinations of the prime factors:
- 20 x 70 = 1
- 21 x 70 = 2
- 22 x 70 = 4
- 20 x 71 = 7
- 21 x 71 = 14
- 22 x 71 = 28
- 20 x 72 = 49
- 21 x 72 = 98
- 22 x 72 = 196
This method systematically lists all the possible combinations of prime factors, guaranteeing we don’t miss any factors.
Real-World Applications of Factors and Divisibility
Don’t be fooled by the seemingly abstract nature of factors and divisibility! These concepts have numerous practical applications that permeate our everyday lives. Let’s explore a few of them:
1. Organizing and Dividing Resources
Think about a group of friends planning a trip. They need to split the costs evenly. Factors come in handy for determining the best way to split expenses. If there are 12 people on the trip and the total cost is $196, they could divide it into groups of 2, 4, or 7 people to simplify the cost-sharing process.
2. Geometry and Proportion
Factors play a crucial role in geometry, often used to determine the dimensions of shapes and solve problems involving ratios and proportions. Take, for example, a rectangular garden with an area of 196 square feet. You can use the factors of 196 to find possible dimensions for the garden, such as 14 feet by 14 feet or 28 feet by 7 feet.
3. Coding and Computer Science
In computer science, factors have applications in cryptography, hashing algorithms, and data organization. By understanding divisibility rules and prime factorization, programmers can write more efficient code and create robust security systems.
Tips and Expert Advice
Mastering factors and divisibility doesn’t require a degree in mathematics, but it does require a strategic approach and some helpful tips. Here are a few pieces of advice to make your factor-finding endeavors more efficient and enjoyable:
- Start with basic divisibility rules: Memorize divisibility rules for 2, 3, 4, 5, 6, 9, and 10. These will quickly eliminate potential factors and save you time.
- Pair up factors: Once you find one factor, its corresponding factor is simply the original number divided by that factor. This streamlines the process.
- Use prime factorization: Prime factorization provides a systematic and reliable way to find all the factors of a number. It’s particularly helpful for larger numbers.
- Practice makes perfect: Like any skill, factor-finding becomes easier with consistent practice. Work through problems of different complexities, and you’ll steadily improve your speed and accuracy.
By implementing these tips and continuously challenging yourself with factor-finding exercises, you’ll become more comfortable and confident in your ability to decompose numbers and understand their underlying structure. Remember, every number holds a story, and by exploring its factors, you unlock a deeper understanding of its nature.
FAQs about Factors and Divisibility
Here are some common questions about factors and divisibility, along with concise and clear answers to guide you:
Q1: What are the factors of 0?
A: The number 0 is divisible by every non-zero number. Therefore, all non-zero numbers are factors of 0.
Q2: Does every number have an even number of factors?
A: No, only perfect square numbers have an even number of factors. All other numbers have an odd number of factors.
Q3: How can I tell if a number is a perfect square?
A: If a number has an odd number of factors, it’s not a perfect square. If it has an even number of factors, it is a perfect square.
Q4: Is 1 a factor of all numbers?
A: Yes, 1 is a factor of every number, including itself.
Q5: What is the greatest common factor (GCF)?
A: The greatest common factor (GCF) of two or more numbers is the largest number that divides all the given numbers evenly.
Factors Of 196
Conclusion
Understanding the factors of 196, along with the broader concepts of divisibility and prime factorization, equips us with powerful tools for navigating the world of numbers. From organizing resources to solving geometric problems and even making advancements in computer science, these concepts have a profound impact on our lives. So, the next time you encounter a number like 196, don’t just see a random collection of digits. See an opportunity to explore its hidden structure, discover its fascinating factors, and unlock a deeper understanding of the world around you.
Do you find the concepts of factors and divisibility intriguing? Are there any specific applications of these concepts that interest you? Share your thoughts in the comments below!






